



















|
|
Particle Deposition Mechanisms: Impaction Particle-Surface Interactions Here a is the radius of the disc, h is the distance between
the surfaces and m is the viscosity of the fluid. Based on Equation (1), the
resistance force becomes infinitely large as
Equating (1) and (2), one finds
and the two disks will come in contact in a finite time.
The Stokes drag on a particle approaching a surface increases rapidly as the
distance from the wall decreases.
For
Equation (4) is valid for
|


|


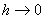 . That implies that the
surfaces could not come in contact. However, the surfaces will indeed come in
contact due to the presence of London - van der Waals force. As noted before,
the van der Waals force per unit area between two plane surfaces is given by
. That implies that the
surfaces could not come in contact. However, the surfaces will indeed come in
contact due to the presence of London - van der Waals force. As noted before,
the van der Waals force per unit area between two plane surfaces is given by
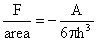
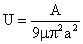
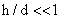 ,
,
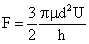
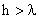 . For smaller h,
Equation (4) is not applicable and the van der Waals force may lead to adherence.
. For smaller h,
Equation (4) is not applicable and the van der Waals force may lead to adherence.