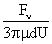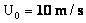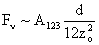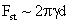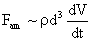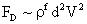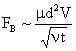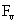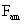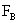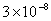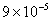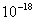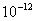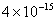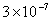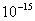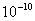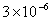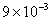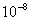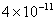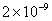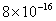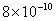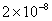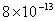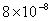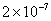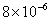|
London-van der Waals Force
Table 1. van der Waals force for a
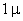 m particles.
For comparison m particles.
For comparison 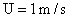 and
a separation of and
a separation of 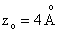 is assumed. is assumed.
| Particle |
Surface |
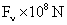 (In air) (In air) |
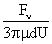 |
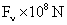 (In water) (In water) |
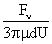 |
| Polystyrene |
Polystynene |
1.2-1.8 |
70-100 |
0.2 |
12 |
| Si |
Si |
13.6-14.4 |
800-850 |
7 |
410 |
| Cu |
Cu |
17 |
1000 |
9.8 |
580 |
| Ag |
Ag |
18 |
1060 |
15.5 |
910 |
Table 2: Variation of Forces (N) versus particle diameter,
d (μm), or a flow velocity of 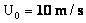 |
|
Van der Waals |
Surface Tension |
Added Mass |
Drag/Lift |
Basset |
| Diameter |
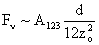 |
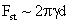 |
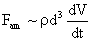 |
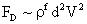 |
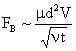 |
| Air |
| d (μm) |
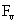 |
 |
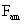 |
 |
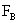 |
| 0.2 |
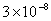 |
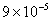 |
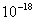 |
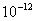 |
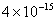 |
| 2 |
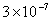 |
 |
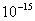 |
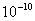 |
 |
| 20 |
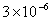 |
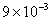 |
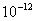 |
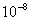 |
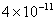 |
| Water |
| d (μm) |
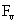 |
 |
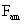 |
 |
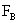 |
| 0.2 |
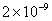 |
___ |
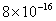 |
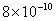 |
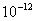 |
| 2 |
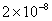 |
___ |
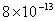 |
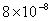 |
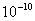 |
| 20 |
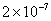 |
___ |
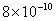 |
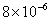 |
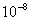 |
Values of van der Waals, surface tension, added mass, drag and Basset forces
acting on a sphere of different sizes moving with a velocity of 10 m/s are
shown in Table 2. For a particle in air, it is seen that the surface
tension force is order of magnitudes larger than the other forces, which is
followed by the van der Waals force. Among the hydrodynamic forces, drag
is the dominating force and the virtual mass and the Basset forces are
negligibly small. In water, the surface tension force is absent and the
drag force acting on large particles beomes comparable with the van der Waals
adhesion force. |
























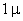 m particles.
For comparison
m particles.
For comparison 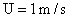 and
a separation of
and
a separation of 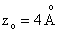 is assumed.
is assumed.
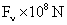 (In air)
(In air)