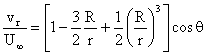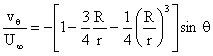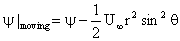

















|

|
| Viscous Flows | |
| Navier-Stokes Equation, Vorticity, Stream Function | Exact Solutions | Drag on Spherical Particles | Creeping Flows | Nonspherical Particles | |


|
|
Creeping Flow Past a Sphere Substituting (12) and (13) into (9), the explicit expression for the stream function becomes
The velocity components are then given by
Figure 2a shows the streamline for the creeping flow around a sphere. Comparing the streamlines of the creeping flow conditions to the potential flow one given by
and is plotted in Figure 2 b, it appears that the stream lines are more dispersed.
Figure 2. Comparison of the streamlines for creeping and potential flows. For moving spheres, the stream function is given by
Figure 3. Comparison of the streamlines for creeping potential flows in a moving frame. For the moving sphere coordinates the corresponding streamlines are shown in Figure 3. Figure 3a shows that the particle appears to be dragging the viscous fluid as it moves, while Figure 3b through suggests that the particle pushes the fluid in the potential flow regime. | ||||


|