


















|

|
| Viscous Flows | |
| Navier-Stokes Equation, Vorticity, Stream Function | Exact Solutions | Drag on Spherical Particles | Creeping Flows | Nonspherical Particles | |


|
Hydrodynamic Forces and Torques for a Nonspherical Particle Oblate Spheroid in a Uniform Flow For brevity, let
Then
The ranges of variation of
For obtaining the flow field around the spheroid, the biharmonic creeping flow equation given by
must be solved. The boundary conditions are
|


|
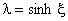 ,
,
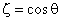
 and z may be expressed as
and z may be expressed as
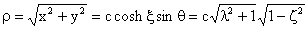
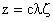
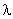 and
and
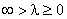 ,
,
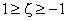
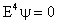
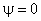 ,
,
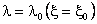
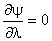 ,
,
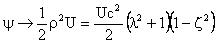 , as
, as