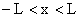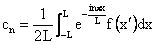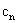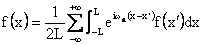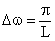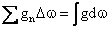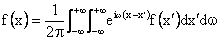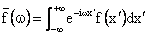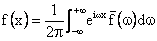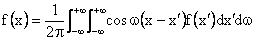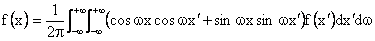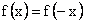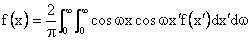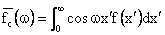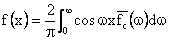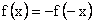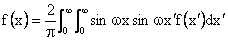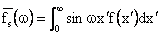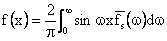Fourier Series

Summary of Fourier Transform Properties

Consider the Fourier Exponential Series in the region

Replacing the expression for the coefficient

In the last step we have defined

As

Define Fourier Transform (Exponential)

The inverse transform is

The above two equations are a Fourier Exponential Transform Pair.

Fourier Integral Representation (FIR) may be restated as

or

For even functions (i.e.

Definition: Fourier-Cos Transform Pair:

For odd functions (i.e.

Definition: Fourier-Sin Transform Pair: