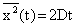


















|
|
Brownian Motions Example: Particle Dispersion and Deposition in a Viscous Sublayer (page 2 of 2) Ounis, Ahmadi and McLaughlin (1991) and Shams and Ahmadi (2000) studied the
dispersion and deposition of nano- and micro-particles in turbulent boundary layer
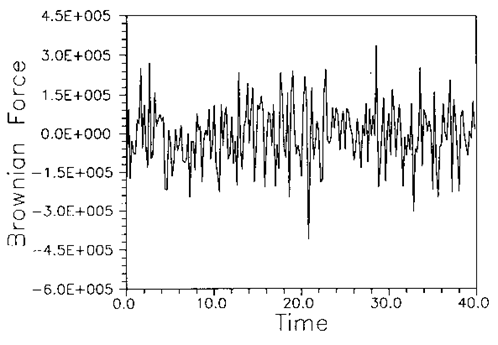
flows. A sample simulated Brownian force for a 0.01
Figure 3. Sample simulated Brownian force. Using the definition of particle diffusivity, D, as given by (10), the variance of the particle position is given by
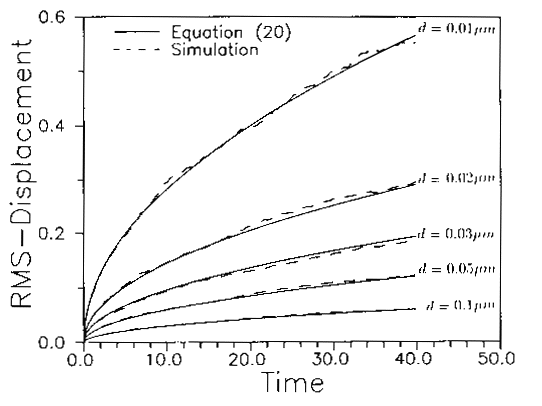
Thus, for a given diffusivity, the variance of the spreading rate of particles may be evaluated from Equation (29). To verify the Brownian dynamic simulation procedure, Ounis et al (1991) studied that special case of a point source in a uniform flow with U+ =U/u* = 1. For different particle diameters, Figure 4 displays the time variation of their simulated root mean square particle position. Here, for each particle size, 500 sample trajectories were evaluated, compiled and statistically analyzed. The corresponding exact solutions given by Equation (29) are also shown in this figure for comparison. It is seen that small nano-meter sized particles spread much faster by the action of the Browning motion when compared with the larger micrometer sized particles. Figure 4 also shows that the Brownian dynamic simulation results for the mean square displacement are in good agreement with the exact solutions.
Figure 4. Sample simulated root-mean square displacement for different particles. |


|


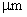 particle is shown in Figure 3.
Here the wall units with
particle is shown in Figure 3.
Here the wall units with 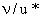 and
and
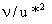 being, respectively, the length
and the time scales are used. Note that the relevant scales the wall layer including
the viscous sublayer are controlled by kinematic viscosity
being, respectively, the length
and the time scales are used. Note that the relevant scales the wall layer including
the viscous sublayer are controlled by kinematic viscosity
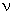 and shear velocity u*.
The random nature of Brownian for is clearly seen form Figure 3.
and shear velocity u*.
The random nature of Brownian for is clearly seen form Figure 3.