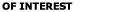


















|
|
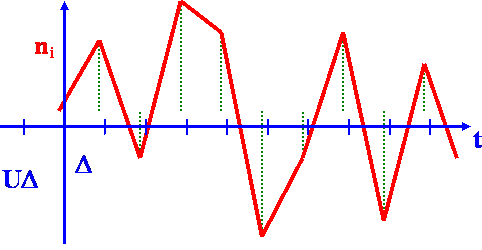
Brownian Motions Computer Simulation Procedure As noted before, the Brownian force n(t) may be modeled as a white noise stochastic process. White noise is a zero mean Gaussian random process with a constant power spectrum given Equation (3). Thus,
The following procedure was used by Ounis and Ahmadi (1992) and Li and Ahmadi (1993).
Choose a time step
The amplitude of the Brownian force then is given by
The entire generated sample of Brownian force need to be shifted by
Figure 2. Numerically simulated Brownian force. |


|


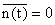 ,
,
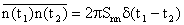
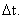 (The time step should much smaller than the particle relaxation time).
Generate a sequence of uniform random numbers,
(The time step should much smaller than the particle relaxation time).
Generate a sequence of uniform random numbers, 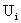 &;(between 0 and 1). Transform pairs of uniform random numbers to pairs of unit variance zero mean Gaussian random numbers.
The can be done using the following transformations:
&;(between 0 and 1). Transform pairs of uniform random numbers to pairs of unit variance zero mean Gaussian random numbers.
The can be done using the following transformations:
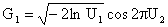
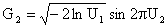
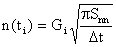
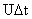 , where U is a uniform random number between zero and one.
, where U is a uniform random number between zero and one.