






















|
|
Reynolds Equation and Mixing Length Model Energy Equation in a Pure Shear Flow The exact (unclosed) energy equation is given by
Note that the last term is zero. For a pure shear flow,
The energy equation then becomes
The energy equations for ( ( ( It is observed that the entire production is for |


|


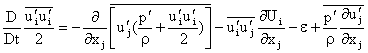
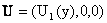 and
and 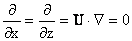 .
.
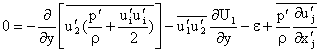 .
.
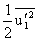 ,
,
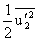 , and
, and
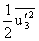 are given as
are given as

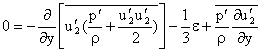
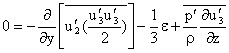
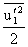 and there is no direct production of
and there is no direct production of 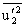 and
and 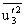 . Therefore,
. Therefore, 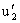 and
and 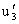 receive their energy from the pressure-velocity interaction terms. That is,
receive their energy from the pressure-velocity interaction terms. That is, 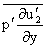 and
and 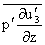 must be positive and
must be positive and 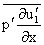 must be negative. In most flows,
must be negative. In most flows, 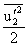 and
and