|
Reynolds Equation and Mixing Length Model
PHENOMENOLOGICAL MODELS FOR TURBULENCE
Reynolds Equation
Since turbulence is a continuum phenomenon, the instantaneous velocity and
pressure fields satisfy the Navier-Stokes equation. i.e.,
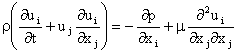 , ,
|
(1)
|
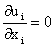 , ,
|
(2)
|
During a turbulent motion 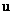 and
p are random functions of space and time. Hence, these may be decomposed into mean and fluctuating parts, i.e. and
p are random functions of space and time. Hence, these may be decomposed into mean and fluctuating parts, i.e.
where 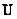 and and
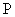 are the mean quantities and are the mean quantities and
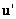 and p' are the
fluctuating parts. Here, a bar on the top of the letter stands for the (time) averaged quantity. That is and p' are the
fluctuating parts. Here, a bar on the top of the letter stands for the (time) averaged quantity. That is
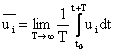 . .
|
(5)
| From the table and the schematic diagram, it is observed that
for 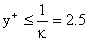 , ,
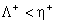 and a turbulent flow cannot exist. and a turbulent flow cannot exist.
|



























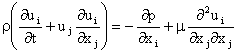 ,
,
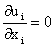 ,
,
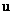 and
p are random functions of space and time. Hence, these may be decomposed into mean and fluctuating parts, i.e.
and
p are random functions of space and time. Hence, these may be decomposed into mean and fluctuating parts, i.e.
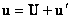 ,
,
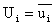 ,
,
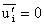 ,
,
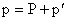 ,
,
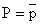 ,
,
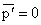 ,
,
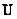 and
and
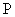 are the mean quantities and
are the mean quantities and
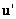 and p' are the
fluctuating parts. Here, a bar on the top of the letter stands for the (time) averaged quantity. That is
and p' are the
fluctuating parts. Here, a bar on the top of the letter stands for the (time) averaged quantity. That is
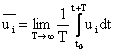 .
.
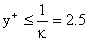 ,
,
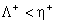 and a turbulent flow cannot exist.
and a turbulent flow cannot exist.