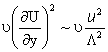|
Features of Turbulence
Energy Spectrum of Turbulence
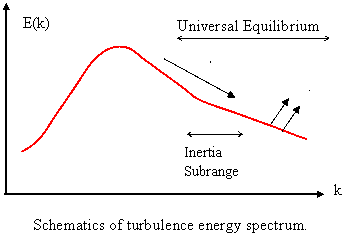
Turbulence has a wide range of length (time) scales. A typical energy
spectrum (Fourier decomposition of energy) is shown in the figure.
Here 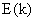 is the
energy spectrum and is the
energy spectrum and 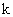 is wave
number (inverse wavelength ( is wave
number (inverse wavelength ( 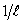 )).
Fluctuation energy is produced at the large eddies (with low wave numbers).
Vortex stretching mechanism then generates smaller and smaller eddies and energy flows down
the spectrum to high wave number region. The energy is mainly dissipated into heat at the
smallest eddies (of the order of the Kolmogorov scales). )).
Fluctuation energy is produced at the large eddies (with low wave numbers).
Vortex stretching mechanism then generates smaller and smaller eddies and energy flows down
the spectrum to high wave number region. The energy is mainly dissipated into heat at the
smallest eddies (of the order of the Kolmogorov scales).
The dissipation rate, 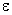 , is
roughly equal to the fluctuation energy production rate. Suppose the large-scale velocity
fluctuation of turbulence is , is
roughly equal to the fluctuation energy production rate. Suppose the large-scale velocity
fluctuation of turbulence is 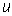 and
the corresponding length scale is and
the corresponding length scale is  . Then
the rate of production (or dissipation) of fluctuation energy is given by . Then
the rate of production (or dissipation) of fluctuation energy is given by
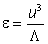
|
(1)
|
Equation (1) implies that large eddies lose a significant fraction of their
energy in a time period of  .
Note that the direct viscous dissipation rate is .
Note that the direct viscous dissipation rate is
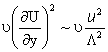
|
(2)
|
and the ratio

|
(3)
|
where

|
(4)
|
is a characteristic Reynolds number.
| 



























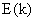 is the
energy spectrum and
is the
energy spectrum and 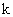 is wave
number (inverse wavelength (
is wave
number (inverse wavelength ( 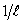 )).
Fluctuation energy is produced at the large eddies (with low wave numbers).
Vortex stretching mechanism then generates smaller and smaller eddies and energy flows down
the spectrum to high wave number region. The energy is mainly dissipated into heat at the
smallest eddies (of the order of the Kolmogorov scales).
)).
Fluctuation energy is produced at the large eddies (with low wave numbers).
Vortex stretching mechanism then generates smaller and smaller eddies and energy flows down
the spectrum to high wave number region. The energy is mainly dissipated into heat at the
smallest eddies (of the order of the Kolmogorov scales).
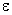 , is
roughly equal to the fluctuation energy production rate. Suppose the large-scale velocity
fluctuation of turbulence is
, is
roughly equal to the fluctuation energy production rate. Suppose the large-scale velocity
fluctuation of turbulence is 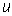 and
the corresponding length scale is
and
the corresponding length scale is  . Then
the rate of production (or dissipation) of fluctuation energy is given by
. Then
the rate of production (or dissipation) of fluctuation energy is given by
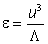
 .
Note that the direct viscous dissipation rate is
.
Note that the direct viscous dissipation rate is