






















|
|
Introduction to Turbulence Modeling VISCOUS FLOW The conservation laws for a continuous media are: Mass:
Momentum:
Angular Momentum:
Energy:
Entropy Inequality:
Constitutive Equation Experimental evidence shows that for a viscous fluid, the stress is a function of velocity gradient. That is
The velocity gradient term may be decomposed as
where
The principle of Material Frame-Indifference of continuum mechanics implies that the stress is generated only by the deformation rate of media and the spin has no effect. This is because both stress and deformation rate tensors are frame-indifferent while spin is not. Thus, the general form of the constitutive equation is given as
For a Newtonian fluid, the constitutive equation is linear and is given as
The entropy inequality imposed the following restrictions on the coefficient of viscosity:
Using the constitutive equation in the balance of momentum leads to the celebrated Navier-Stokes equation. For an incompressible fluid the Navier-Stokes and the continuity equations are given as
These form four equations for evaluating four unknowns
|


|


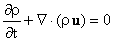
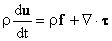
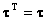

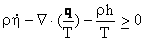
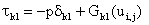

 is
the spin tensor. These are given as
is
the spin tensor. These are given as


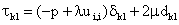
 ,
,
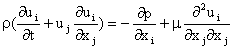 ,
,
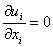
 .
.