|
Introduction to Turbulence Modeling Comparison of Model Predictions
Conclusions (Existing Models)
- Available models can predict the mean flow properties with reasonable accuracy.
Small adjustments of parameters are sometimes necessary.
- First-order modeling gives reasonable results only when a single length and
velocity scale characterizes turbulence.
- The
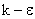 model gives
relatively accurate results when a scalar eddy viscosity is sufficient to
characterize the flow. That is there is no preferred direction for example
through the action of a body force. model gives
relatively accurate results when a scalar eddy viscosity is sufficient to
characterize the flow. That is there is no preferred direction for example
through the action of a body force.
- The stress transport models have the potential to most accurately represent
the mean turbulent flow fields.
Deficiencies of Existing Models
- Adjustments of coefficients are sometimes needed.
- The derivation of the models are somewhat arbitrary.
- There is no systematic method for improving a model when it loses its accuracy.
- Models for complicated turbulent flows (such as multiphase flows) are not available.
- Realizability and other fundamental principles are sometimes violated.
- For example, the transport equations for
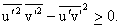
| 












































