Postdoctoral Associate
Yale University, USA , Ecology & Evolutionary Biology
Mentor: Prof. C. Brandon Ogbunu
Committed lecturer and Mathematician with varied applied mathematical research interests and a passion for constructive and efective teaching methods to promote a stimulating learning environment. My research interests are focused on deepening ourunderstanding of data-driven analysis methods for dynamical systems. I would like to see both mathematical and statistical view of data science. I plan to explore and improve the data analysis tools, and like to find potential applications of those tools.

Yale University, USA , Ecology & Evolutionary Biology
Mentor: Prof. C. Brandon Ogbunu
Clarkson University, USA, Electrical and Computer Engineering
Mentor: Prof. Erik M. Bollt
Clarkson University, USA, Department of Mathematics
University of North Florida,USA, Department of Mathematics and Statistics
University of Colombo, Sri Lanka, Mathematics Unit
Uva Wellassa University of Sri Lanka,Faculty of Management
University of Colombo, Sri Lanka, Department of Mathematics
Ph.D. in Mathematics
Clarkson University, USA
Dissertation: “Learning features of Dynamical Systems by Data Driven Analysis Methods”
Summer school(7 Credit) for teaching college level STEM courses
SIGTA, Clarkson University, USA
Master of science in Applied Mathematics
University of North Florida, USA
Master of science in Financial Mathematics
University of Colombo, Sri Lanka
Bachelor of science (Honours) in Mathematics
University of Colombo, Sri Lanka
My research interests lie in the field of applied mathematics. I would like to study complex systems (probably non-linear dynamical systems) and understand the global dynamics of the system by using equation-free modeling. Dynamical systems, Choas theory, Manifold learning methods(Diffusion map), Machine learning, Koopman theory and it's numerical aproximations(DMD), Causal Inference, Information theory, and probability theory are the major tools in data-driven analysis in these complex systems. I like to apply these tools in any field. I always open to learning and building new tools from mathematics, statistics or computer science and like to apply and analyze them with deferent fields.
Randomized Projection Learning Method for Dynamic Mode DecompositionMathematics 2021
Mathematics, Volume 9, Issue 21: 2803
November 2021
|
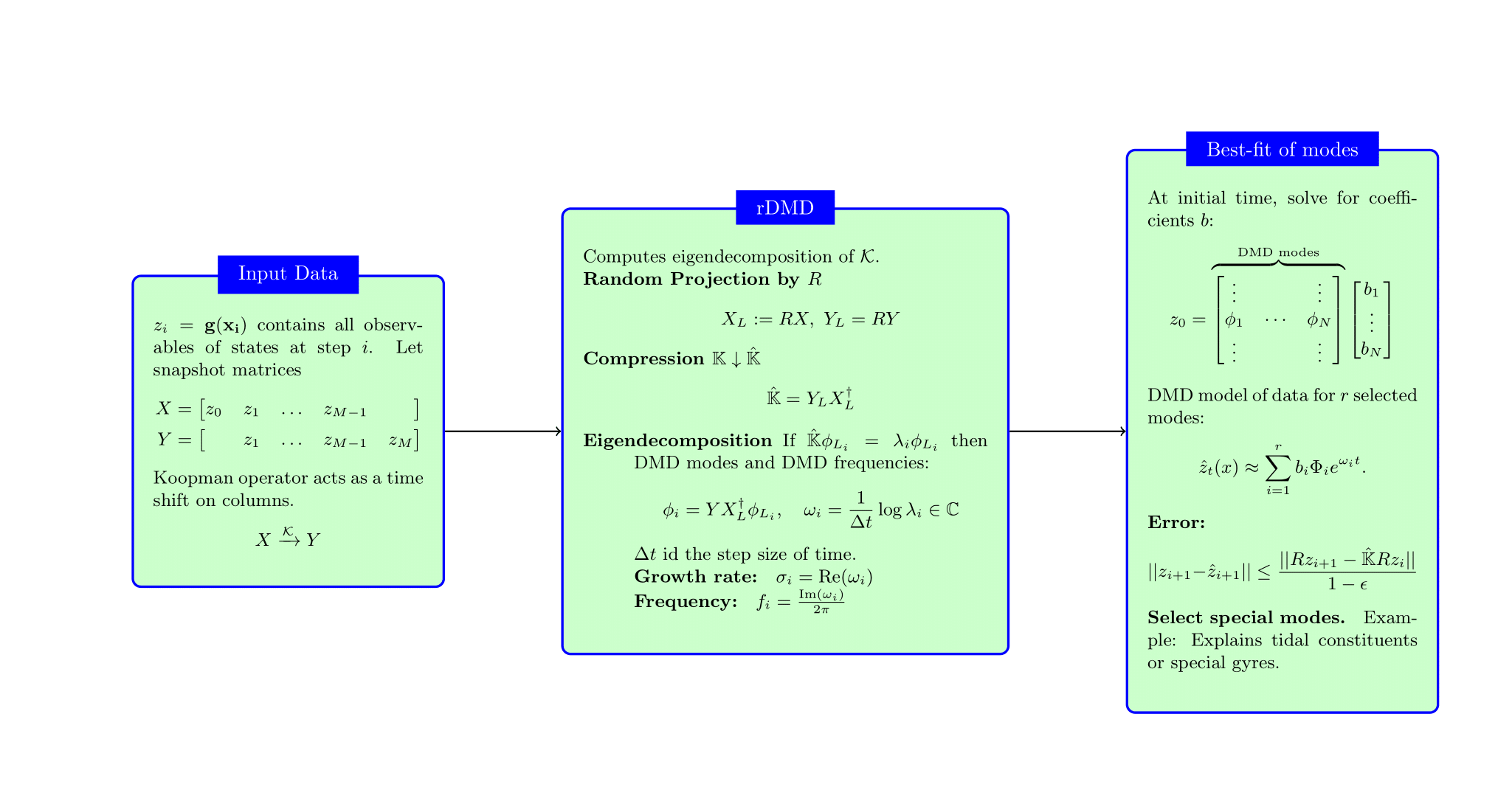
A data-driven analysis method known as dynamic mode decomposition (DMD) approximates the linear Koopman operator on a projected space. In the spirit of Johnson--Lindenstrauss lemma, we will use a random projection to estimate the DMD modes in a reduced dimensional space. In practical applications, snapshots are in a high-dimensional observable space and the DMD operator matrix is massive. Hence, computing DMD with the full spectrum is {expensive}, so our main computational goal is to estimate the eigenvalue and eigenvectors of the DMD operator in a projected domain. We~generalize the current algorithm to estimate a projected DMD operator. We focus on a powerful and simple random projection algorithm that will reduce the computational and storage costs. While, clearly, a random projection simplifies the algorithmic complexity of a detailed optimal projection, as we will show, the results can generally be excellent, nonetheless, and the quality could be understood through a well-developed theory of random projections. We will demonstrate that modes could be calculated for a low cost by the projected data with sufficient dimension.
Keywords: Koopman operator; dynamic mode decomposition~(DMD); Johnson-Lindenstrauss lemma; random projection; data-driven method
On Geometry of Information Flow for Causal InferenceEntropy 2020
Entropy, Volume 22, Issue 4:396
April 2020
|

|
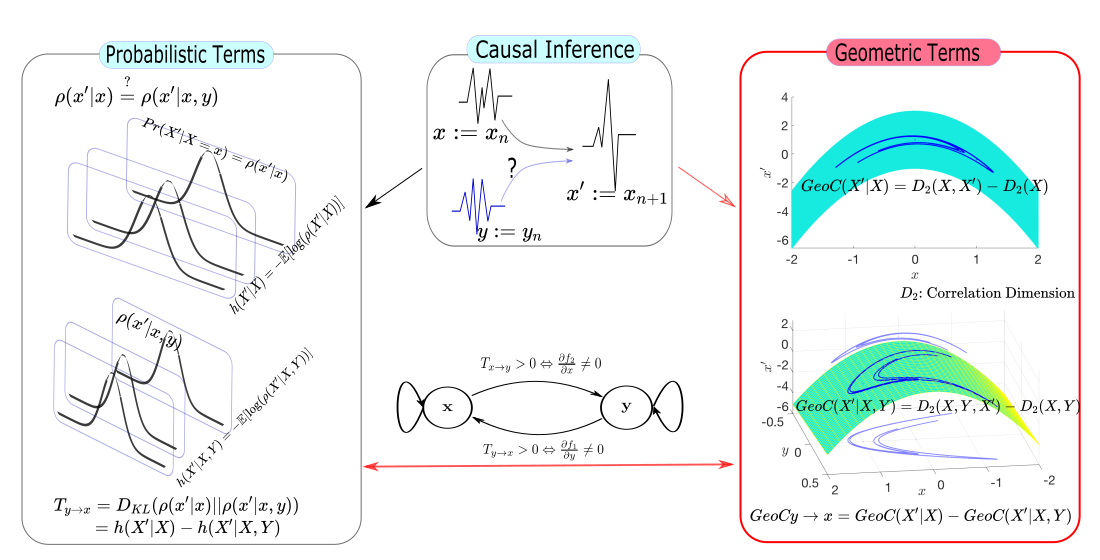
Causal inference is perhaps one of the most fundamental concepts in science, beginning originally from the works of some of the ancient philosophers, through today, but also weaved strongly in current work from statisticians, machine learning experts, and scientists from many other fields. This paper takes the perspective of information flow, which includes the Nobel prize winning work on Granger-causality, and the recently highly popular transfer entropy, these being probabilistic in nature. Our main contribution will be to develop analysis tools that will allow a geometric interpretation of information flow as a causal inference indicated by positive transfer entropy. We will describe the effective dimensionality of an underlying manifold as projected into the outcome space that summarizes information flow. Therefore contrasting the probabilistic and geometric perspectives, we will introduce a new measure of causal inference based on the fractal correlation dimension conditionally applied to competing explanations of future forecasts, which we will write $GeoC_{y\rightarrow x}$. This avoids some of the boundedness issues that we show exist for the transfer entropy, $T_{y\rightarrow x}$. We will highlight our discussions with data developed from synthetic models of successively more complex nature: then include the Hénon map example, and finally a real physiological example relating breathing and heart rate function.
Keywords: Causal Inference; Transfer Entropy; Differential Entropy; Correlation Dimension; Pinsker's Inequality; Frobenius-Perron operator.
To infer transfer operators from data is usually take as a classical problem that hinges on the Ulam method. The usual description is in terms of projection onto basis functions that are characteristic functions supported over a fine grid of rectangles, that we have previously called the Ulam-Galerkin method when taken in terms of finite time. Here, we present that the same problem can be understood by statistical density estimation formalism. In these terms, the usual Ulam-Galerkin approach is a density estimation by the histogram method. This perspective allows us other methods such as spectral density estimation, Kernel density estimation, etc. However, this is not the only popular method of density estimation, and we point out inherent efficiencies available by the popular kernel density estimation method, and this general phrasing of the problem allows for analysis of bias and variance, toward a discussion of the mean square error for example
Learning high dimensional nonlinear dynamical systems multivariate time series data, without knowing the governing equation is a trending topic in the field of dynamical systems, fluid dynamics, aerodynamics, neuroscience, financial trading markets, multimedia, etc. In the spirit of random projection theory and especially the Johnson-Lindenstrauss theorem, we will re-interpret a major tool known as Dynamic Mode Decomposition (DMD) and its extensions. Simple and computationally efficient random projections improve aspects of the DMD, the Extended DMD (EDMD), and also kernelized DMD approximations of the Koopman operator. The Johnson-Lindenstrauss Lemma provides a theoretical framework for random feature selection by random projection matrices.
Oceanic flow around the Strait of Gibraltar comprises dynamic sub-mesoscale features arising due to topographic and tidal forcing, instabilities, and strongly nonlinear hydraulic processes, all governed by nonlinear equations of fluid motion. The purpose of this study is to isolate dominant features from 3D MIT general circulation model simulations and to investigate their physics. To this end, we use the Dynamic Mode Decomposition (DMD) that decomposes the sequence of simulation snapshots into a sum of Koopman modes: spatial profiles with well-defined exponential growth/decay rates and oscillation frequencies. To identify known features, we correlate identified DMD modes with the tidal forcing and demonstrate that DMD is able to non-parametrically detect the prominent waves known to occur in the western Mediterranean. Additionally, the analysis reveals previously undocumented Kelvin waves and demonstrates that meandering motions in the Atlantic Jet entering the Mediterranean Sea are associated with the diurnal tidal forcing. The DMD thus recovers the results obtained by classical harmonic analysis of tidal constituents, and also highlights features that have eluded attention so far, suggesting that DMD could be a useful part of an oceanographer's toolbox.
We applied Dynamic Mode Decomposition (DMD) to identify flow constituents in a three-dimensional simulation of tidal flows through the Strait of Gibraltar over a six-day period. DMD managed to isolate well-known tidal patterns, such as the Western Alboran Gyre, the twelve-hour lunar tide cycle (M2), and the tidal bore discharging Atlantic waters into the Mediterranean. Additionally, the DMD modes were able to clarify the structure of a recurrent flow pattern occurring as the water passes the Camarinal Sill just to the Atlantic side of Gibraltar.
DNA graph structures can self-assemble from branched junction molecules to yield solutions to computational problems. For a given graph $G$, the self-assembled structure represents a thickened graph $F(G)$ containing $G$ as a deformation retract. We show that for every postman tour $\tau$ in a connected $3$-valent (multi)graph $G$ there exists a thickened graph $F(G)$ with a reporter strand $\sigma$ which contains $\tau$. In cases where the postman tour $\tau$ and the reporter strand $\sigma$ are non-identical, DNA self-assembly may not be able to replicate the tour without including an extra cycle. Further reduction of the reporter strands to isolate the postman tour contained within $\sigma$ would yield all non-maximal optimal postman tours of G.
By using iterative three-degree perturbations, any graph can be represented as a self-assembled DNA graph structure of three armed junction molecules. In representing these graph structures as deformation retracts of closed compact DNA manifolds, a single strand can be identified which traverses each edge of the graph structure at least once. We show various applications of the property to traditional graph theory problems, and consider weighting algorithms and their applications to DNA computing.
As per business entities, customer satisfaction is the growing fact towards profit maximization and competitiveness. So, it tends to increase researcher’s interest in the topic of Service Quality. It always depends on the behavior of the stakeholders of the business. Especially, as it is being used to measure the level of satisfaction of the customers. Evaluating this satisfactory level is basically finding a Mathematical model for the behavior of the customers. Here, we try to quantify the level of service quality via mathematical modeling approach.
When selecting a suitable tool, the vagueness of the customers’ opinions has to be considered. The logical tools that people can rely on are generally considered the outcome of a bivalent logic, but the problems posed by real-life situations and human thought processes and approaches to problemsolving are by no means bivalent. So, fuzzy sets have to be used for the representation of human opinion. Neural network can be used to train the human behavioral patterns and it can be used to find the relationship between the respondent’s view of the service quality criterion and overall ranking of the service. Therefore, fuzzy model & Hybrid model (i.e. combine fuzzy logic with neural network) are used in this research. A case study is done to find out the validity of the proposed model.
It is important to identify recession before a country becomes a recession state. So development of forecast models is an important subject area. Leading economic indicators change before the economy changes and can be used to predict what the economy will be like in the future. So, recession can be forecast using leading economic indicators and neural networks can detect relationships among the selected leading indicators and the recession signals. In recent years, neural networks have been increasingly used for a wide variety of applications. Due to the structure of the neural network, a reasonably large number of indicators can be used. In this project, seven leading indicators of USA were used. The result shows that this model could predict the recession with 90 percent of confidence.
In this section, I listed some projectes and homework solutions complete as a student.
I would be happy to talk to you if you need my assistance.