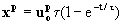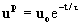Clarkson U. | CRCD | ME 637 | Aerosols

Review of Turbulence and Turbulence Modeling


Aerosols

Introduction to Aerosols \| Drag, Lift Forces \| Aerosol Kinetics \| Virtual Mass, Basset Forces & BBO Equation \| Nonspherical Particles \| Brownian Motions \| Particle Deposition Mechanisms \| Electrodynamics \| Aerosol Coagulation \|

Aerosol Kinetics

Terminal Velocity

For a particle starting from rest, the solution to equiaton 2 is given as

(5)

where u^ƒ is assumed to be a constant vector. For u^ƒ=0 and large t, the terminal velocity of particle u^t is given by

(6)

Table 7: Relaxtion time τ for a unit density particle in the air(p=1 atm, T=20°C)

Diameter, µm u^t=τ g τ (sec) Stop Distance
u_o = 1m/s Stop Distance
u_o=10m/s

0.05 0.39 µm/s 4x10^-8 0.04 µm 4x10^-4 mm

0.1 0.93 µm/s 9.15^-8 0.092 µm 9.15x10^-4 mm

0.5 10.1 µm/s 1.03x10^-6 1.03 µm 0.0103 mm

1 35 µm/s 3.57x10^-6 3.6 4µm 0.0357 mm

5 0.77 mm/s 7.86x10^-5 78.6 µm 0.786 mm

10 3.03 mm/s 3.09x10^-4 309 µm 3.09 mm

50 7.47 cm/s 7.62x10^-3 7.62 mm 76.2 mm

Stopping Distance

In the absence of gravity and fluid flow, for a particle with an initial veolocity of u, the solution to 2 is given by

(7)

(8)

where x^p is the position of the particle. As t→&infin, u^p→0 and

(9)

is known as the stopping distance of the particle. For an initial veolocity of 1000 cm/s, the stop distance for various particles is listed in Table 7.

Dr. Goodarz Ahmadi | Turbulence & Multiphase Fluid Flow Laboratory | Department of Mechanical & Aeronautical Engineering
Copyright © 2002-2005 Dr. Goodarz Ahmadi. All rights reserved.
Potsdam, New York, 13699
ahmadi@clarkson.edu