






















|
|
Particle Deposition Mechanisms Mass Diffusion In this section the mass transfer process is described. The Brownian diffusion of small particles and Fick's law are first discussed. This is followed by the presentation of a number of applications. Brownian Diffusion Small particles suspended in a fluid undergo random translational motions due to molecular collisions. This phenomenon is referred to as the Brownian motion. The Brownian motion leads to diffusion of particles in accordance with Fick's law. i.e., |
|
|||||||||
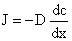
| (1) |
where c is the concentration, J is the flux, and D is the diffusion coefficient. When the effect of particle inertia is negligible, using (1) in the equation of conservation of mass for particles leads to

| (2) |
where v is the fluid velocity vector. The particle mass diffusivity is given by

| (3) |
where  ). The
diffusive may be restated as
). The
diffusive may be restated as

| (4) |
where m is the mass of the spherical particle and
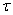 is its relaxation time.
is its relaxation time.


