Drag force and Drag Coefficient

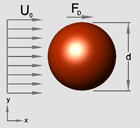
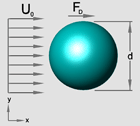
A particle suspended in a fluid is subjected to a number of hydrodynamic forces. For low Reynolds number flows, the Stokes drag force on a spherical particle is given by

where d is the particle diameter, µ is the coefficient of viscosity and U is the relative velocity of the fluid with respect to the particle. Equation (1) may be restated as

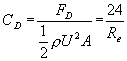(2)

In Equation (2), ρ is the fluid (air) density, 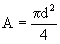is the cross sectional area of the spherical particle, and

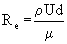(3)

is the Reynolds number. The Stokes drag is applicable to the creeping flow regime (Stokes regime) with small Reynolds numbers (R_e<0.5). At higher Reynolds numbers, the flow of the drag coefficient deviates from Equation 2. Figure 1, below, shows the variation of the drag coefficient for a sphere in a range of Reynolds numbers.