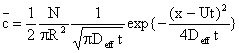|
|
Particle Deposition Mechanisms: Mass Diffusion Diffusion in a Stream in a Tube The equation governing the convective diffusion in a tube is given as
with
where U is the mean velocity in the tube. In a coordinate system moving with the mean fluid velocity U, Equation (54) may be restated as
where the axial diffusion
For zero flux to the wall, the boundary condition at the tube surface is given as
As a first approximation,
Now solving Equation (56) for c, it follows that
where
Using (59) in (60), the value of
The total flow of substance across the pipe then is given by
The flux
has the same form as Fick's law with an effective diffusivity
In the next approximation we drop the assumption that
Equation (65) is applicable if the Peclet number,
If a certain amount N of substance is introduced at
Then the solution to Equation (65) is given as
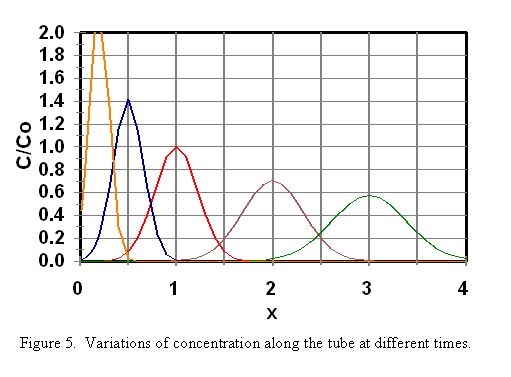
Variation of concentration as a function of space and time are shown in Figure 5. It is seen that the concentration travels like a wave but also dispersed along it path.
|


|


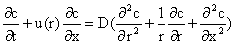
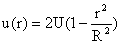

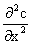 is neglected.
is neglected.
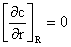
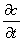 in the moving
frame is negligibly small and
in the moving
frame is negligibly small and

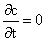

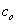 may be evaluated and then
may be evaluated and then
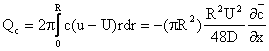
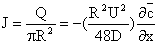

 thus
thus

 satisfy
satisfy

 , that is
, that is