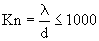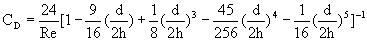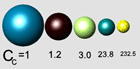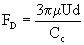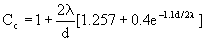|
Drag Force
|
Wall Effects on Drag Coefficient
For a particle moving near a wall, the drag force varies with the
distance of the particle from the surface. Brenner (1961) analyzed
the drag acting on a particle moving toward a wall under the creeping
flow condition as shown in figure 4a. To the first order, the
drag coefficient is given as
 |
(7) |
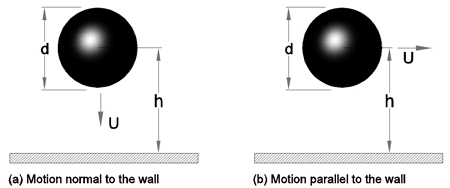
For a particle moving parallel to the wall as shown in Figure 4b, the
Stokes drag force needs to be modified. For large distances
from the wall, Faxon (1923) found
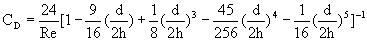 |
(8) |
|
|
| Drag Force Calculation Models |
 |

Parallel Wall Effects
|
 |
Vertical Wall Effects |
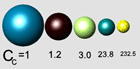
Cunningham Correction Factor
|
|
Cunningham Correction Factor
For very small particles, when the particle size becomes comparable with the gas mean free path,
slip occurs and the expression for drag must be modified accordingly.
Cunningham obtained the needed correction to the Stokes drag force:
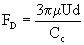 |
(9) |
where the Cunningham correction factor C is given by
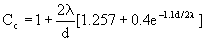 |
(10) |
Here, λ denotes the molecular mean free path in the
gas. Note that Cc > 1 for all values of d and λ.
Figure 5 shows the variation of Cunningham correction factor with Knundsen number.
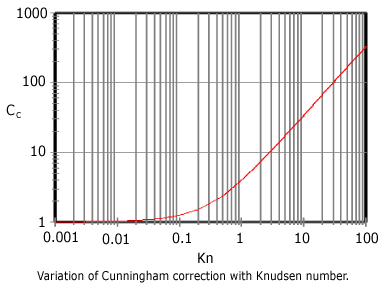 It is seen that Cc is about 1 for Kn < 0.1 and increases
sharply as Kn increases beyond 0.5. Table 4 illustrates the
variation of the Cunningham correction factor with particle diameter
in air under normal pressure and temperature conditions with λ = 0.07
µm. Equation 10 is applicable to a wide range of
It is seen that Cc is about 1 for Kn < 0.1 and increases
sharply as Kn increases beyond 0.5. Table 4 illustrates the
variation of the Cunningham correction factor with particle diameter
in air under normal pressure and temperature conditions with λ = 0.07
µm. Equation 10 is applicable to a wide range of
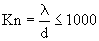
that covers slip, transition, and part of free molecular flows. However,
the particle Reynolds number Mach (based on relative velocity)
should be small.
Table 4: Variations of Cc with d for λ = 0.07 µm
| Diameter, µm | Cc |
|---|
| 10 µm |
1.018 |
| 1 µm |
1.17 |
| 0.1 µm |
3.01 |
| 0.01 µm |
23.77 |
| 0.001 µm |
232.5 |
|