






















|
|
Coagulation of Particles Coagulation of Monodisperse Spheres Equation (1) may be restated as
The concentration field then is given by
|
|
|||||||||||||
The flux to surface of the reference particle is given by

| (6) |
where  is the total flux to the surface of the reference particle per unit time. Using (5), it follows that
is the total flux to the surface of the reference particle per unit time. Using (5), it follows that

| (7) |
For large  ,
,

| (8) |
In reality, the reference particle is not fixed and is diffusing itself. The relative diffusivity of two particles is sum of their diffusivities. That is according to Einstein's equation
 ,
,
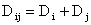
| (9) |
In the derivation of (9) it is assumed that
 , the reference particle
collides with
, the reference particle
collides with

| (10) |
particles. Here,
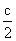 collisions if
all the particles collide once. Assuming that the particles stick to each
other upon collision, it follows that
collisions if
all the particles collide once. Assuming that the particles stick to each
other upon collision, it follows that

| (11) |
where

| (12) |
is the collision frequency function of coagulation constant.
Equation (11) may be solved. i.e.,
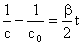
| (13) |
or
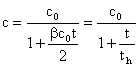
| (14) |
Here, 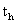 is the
half-value time, which is the time that the concentration becomes half of its
original value.
is the
half-value time, which is the time that the concentration becomes half of its
original value.




