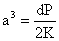|

|
| Particle Adhesion | |
| Van der Waals Force | JKR and Other Adhesion Models | Particle Adhesion & Removal | Effects of Charge | Effect of Humidity | Ultrasonic and Megasonic Cleaning | |


|
|
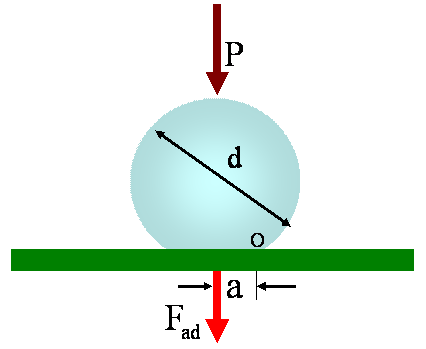
JKR and Other Adhesion Models Figure 1 shows the schematic of a particle of diameter d
attached to a flat surface. Here P is the external force exerted
on the particle, a is the contact radius and
Figure 1: Spherical particle of diameter d attached to a flat, horizontal surface. JKR Model Johnson-Kandall-Roberts (1971) developed a model (The JKR Model) that included the effect of adhesion force on the deformation of an elastic sphere in contact to an elastic half space. Accordingly, the contact radius is given as
Here
In Equation (2), E is the elastic modulus, In the absence of surface forces,
|


|
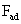 is the adhesion force.
The classical Hertz contact theory provides for the elastic deformation of bodies in contact,
but neglects the adhesion force. Several models for particle adhesion to flat surfaces
were developed in the past that improves the Hertz model by including the effect of adhesion (van der Waals) force.
is the adhesion force.
The classical Hertz contact theory provides for the elastic deformation of bodies in contact,
but neglects the adhesion force. Several models for particle adhesion to flat surfaces
were developed in the past that improves the Hertz model by including the effect of adhesion (van der Waals) force.
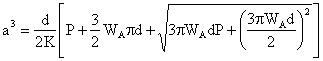
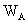 is the thermodynamic work of
adhesion, and K is the composite Young's modulus given as
is the thermodynamic work of
adhesion, and K is the composite Young's modulus given as

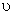 is
the Poisson ratio, and subscript 1 and 2 refer to the materials of the sphere and substrate.
is
the Poisson ratio, and subscript 1 and 2 refer to the materials of the sphere and substrate.
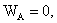 and
Equation (1) reduced to the classical Hertz model. That is
and
Equation (1) reduced to the classical Hertz model. That is