Vorticity Equations

Taking the curl of the Navier-Stokes equation given by (3), we find the vorticity transport equation. That is

.

(6)

Here the vector identity

.

(7)

is used. Noting that

.

(8)

Equation (6) may be restated as

.

(9)

or

.

(10)

where d is the deformation rate tensor.
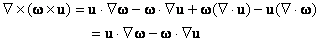