|
Vorticity Equations During a turbulent motion
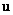 and and
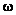 become random
functions of space and time, and they may be decomposed into a mean and fluctuating
parts. i.e., become random
functions of space and time, and they may be decomposed into a mean and fluctuating
parts. i.e.,
where 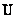 and and
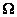 are the mean
quantities and are the mean
quantities and 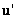 and
and 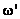 are
the fluctuating parts. As was noted before, a bar on the top of the letter
stands for the (time) averaged quantity. are
the fluctuating parts. As was noted before, a bar on the top of the letter
stands for the (time) averaged quantity.
Substituting (11) and (12) into Equation (10) after
averaging we find the mean vorticity transport equation. That is
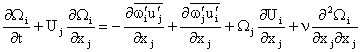 . .
|
(13)
|
Subtracting (13) from (10) leads to the equation for the vorticity fluctuation
field. That is
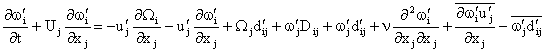 . .
|
(14)
|
Equation (14) may be used to derive the mean square vorticity or dissipation
rate transport equations.
|



























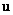 and
and
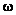 become random
functions of space and time, and they may be decomposed into a mean and fluctuating
parts. i.e.,
become random
functions of space and time, and they may be decomposed into a mean and fluctuating
parts. i.e.,
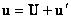 ,
,
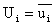 ,
,
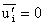 ,
,
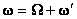 ,
,
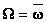 ,
,
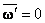 ,
,
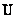 and
and
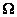 are the mean
quantities and
are the mean
quantities and 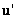 and
and 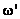 are
the fluctuating parts. As was noted before, a bar on the top of the letter
stands for the (time) averaged quantity.
are
the fluctuating parts. As was noted before, a bar on the top of the letter
stands for the (time) averaged quantity.
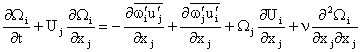 .
.
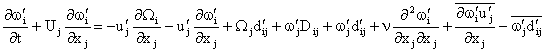 .
.