|
Reynolds Equation and Mixing Length Model
The probabilistic (ensemble) average is defined as
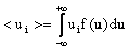
|
(6)
|
where 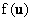 is the
probability density function of is the
probability density function of 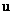 . Ergodicity
assumption implies that the time average and ensemble average are equal. Hence, . Ergodicity
assumption implies that the time average and ensemble average are equal. Hence,
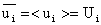
|
(7)
|
Note that the ergodicity hypothesis has not been proven for turbulence; however,
it is commonly used to relate the theoretical results to the experimental data.
It is also well known that while
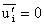 , ,
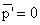 , ,
About a century ago, Reynolds suggested to use the
decomposition given by (2) and (3) into the Navier-Stokes equation and
average the resulting equation. Noting that
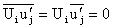 , ,
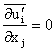 , ,
|
(9)
|
it follows that
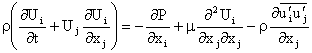 , ,
|
(10)
|
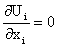 , ,
|
(11)
|
|



























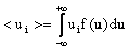
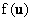 is the
probability density function of
is the
probability density function of 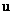 . Ergodicity
assumption implies that the time average and ensemble average are equal. Hence,
. Ergodicity
assumption implies that the time average and ensemble average are equal. Hence,
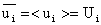
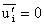 ,
,
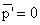 ,
,
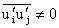 ,
,
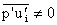 ,
,
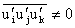 .
.
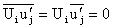 ,
,
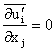 ,
,
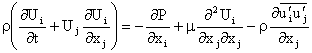 ,
,
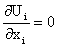 ,
,