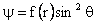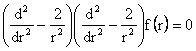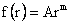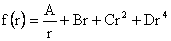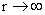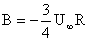|

|
| Viscous Flows | |
| Navier-Stokes Equation, Vorticity, Stream Function | Exact Solutions | Drag on Spherical Particles | Creeping Flows | Nonspherical Particles | |


|
|
Creeping Flow Past a Sphere Now let
Equation (2) then becomes
Equation (4) is an Euler differential equation, which accepts a power law solution. That is
Substituting (6) into (5), it follows that
Roots of the characteristic equation given by (7) are
Thus, the general solution is given as
Using (4), the boundary conditions given by Equation (3) becomes
Comparing the expression given by (9) as
Using boundary conditions given by (10), it follows that
|


|