|

|
| Viscous Flows | |
| Navier-Stokes Equation, Vorticity, Stream Function | Exact Solutions | Drag on Spherical Particles | Creeping Flows | Nonspherical Particles | |


|
Creeping Flows The creeping flow of an incompressible Newtonian fluid satisfies the Stokes equation
and the equation of continuity given as
Taking the divergence of (1) and using (2), in the absence of body force one finds
Reciprocity Theorem Suppose
where S is a closed surface bounding any fluid volume. (See Happel and Brenner, page 85 for the proof). Minimum Energy Dissipation Theorem (Helmholtz):The dissipation rate in creeping flow is less than any other incompressible, continuous motion consistent with the same boundary condition. (See Happel and Brenner for the proof.) |


|
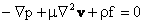
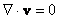
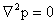
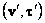 are
two independent solutions (velocity and stress) to (1) and (2). Then
are
two independent solutions (velocity and stress) to (1) and (2). Then