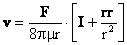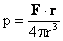|
Creeping Flows
Point Force Solution
Consider the response of the Stokes equation to a point force exerted at the origin. Equation (1) and (2) may be rewritten as
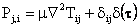
|
(5)
|
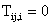
|
(6)
|
The general solution to (5) and (6) in an unbounded domain is given as
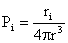
|
(7)
|
Here, 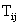 is
referred to as the Oseen tensor. The solution in a two-dimensional flow is given by is
referred to as the Oseen tensor. The solution in a two-dimensional flow is given by
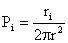
|
(8)
|
Using the Green theorem, the velocity vector may be represented as
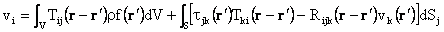
|
(9)
|
where
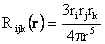
|
(10)
|
and
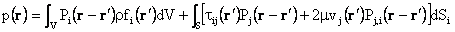
|
(11)
|
Equations (9) and (11) give the velocity and the pressure fields for
arbitrary given distribution of stress and velocity on solid surface boundaries.
For an unbounded flow and for a point force
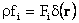 , from (9) and (11)
it follows that , from (9) and (11)
it follows that
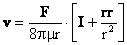
|
(12)
|
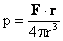
|
(13)
|
which is referred to as a Stokeslet.
| 


























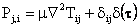
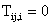
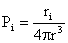
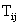 is
referred to as the Oseen tensor. The solution in a two-dimensional flow is given by
is
referred to as the Oseen tensor. The solution in a two-dimensional flow is given by
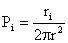
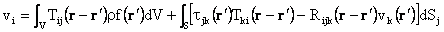
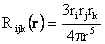
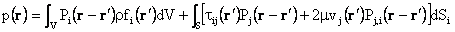
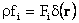 , from (9) and (11)
it follows that
, from (9) and (11)
it follows that