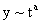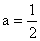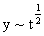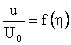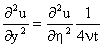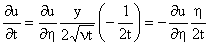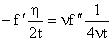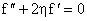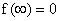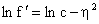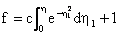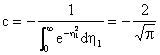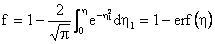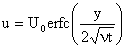|

|
| Viscous Flows | |
| Navier-Stokes Equation, Vorticity, Stream Function | Exact Solutions | Drag on Spherical Particles | Creeping Flows | Nonspherical Particles | |


|
|
Exact Solutions to the Navier-Stokes Equation Similarity Solution (Group Theory) Let
Equation (1) implies that
Thus,
Now introducing the similarity variables
we find
Substituting (9) and (10) in Equation (1), we find
or
Boundary and initial conditions (2)-(4) in terms of the similarity variables become
From Equation (12), it follows that
or
where the first boundary condition in (13) is used. The second boundary condition implies that
Equation (15) then becomes
or
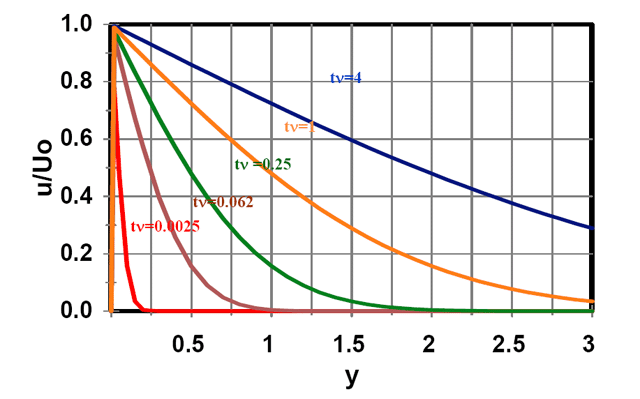
The time variations of the velocity profile as predicted by Equation (18) are shown in Figure 2. Figure 2. Time variations of velocity profile.
|


|