Incompressible Viscous Flows

Plane Stagnation Flows

 Consider a steady plane stagnation flow shown in Figure 1. For steady plane flow the Navier-Stokes equation reduces to

or

Figure 1. Schematics of plane stagnation flow.

Potential stagnation plane flow is described by

We look for a solution of the form

Then

Using (4) and (5), equation (2) becomes

or

Integrating (7) we find

The boundary conditions are:

At

At large y, Equations in (3) holds.

That is

As

Using (12) we find

Thus

Introducing a change of variable (Schlichting,1960)

Equation (14) may be restated as

subject to boundary conditions

as

Graphical representation of the numerical solution is shown in Figure 2. Additional details of the solution are discussed by Schlichting (1960). Accordingly,

At

.

Hence, the boundary layer thickness is given by

.
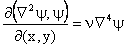
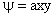
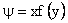
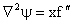
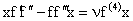
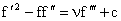
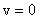
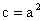
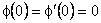
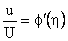