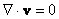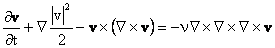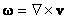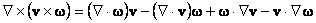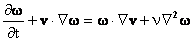

















|

|
| Viscous Flows | |
| Navier-Stokes Equation, Vorticity, Stream Function | Exact Solutions | Drag on Spherical Particles | Creeping Flows | Nonspherical Particles | |


|
|
Incompressible Viscous Flows For an incompressible fluid, the continuity equation and the Navier-Stokes equation are given as
Using a vector identity, Equation (2) may be restated as
Define vorticity
and taking curl of (3) we find
Noting that curl of gradient is zero and
Equation (5) may be restated as
Equation (7) is the vorticity transport equation. It shows that in addition to being convected and diffused, vorticity is also generated by the first on the right hand side of Equation (7) by a vortex stretching mechanism. |


|