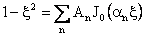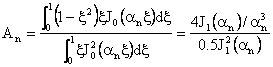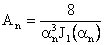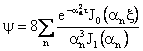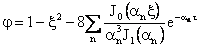Exact Solutions to the Navier-Stokes Equation
Unsteady Flow in a Tube
The boundary condition is
|
(40)
|
with the initial conditions
|
(41)
|
Let
|
(42)
|
Equation (39) reduces to
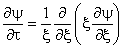
|
(43)
|
The boundary and initial conditions (40) and (41) now become
At 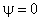 . .
|
(44)
|
At 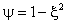 . .
|
(45)
| To determine the solution, the method of separation of variables is used. That is let
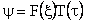
|
(46)
|
Equation (43) then becomes
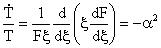 . .
|
(47)
|
From Equation (47), it follows that
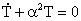 , ,
|
(48)
|
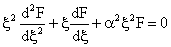 . .
|
(49)
|
The solutions to Equations (48) and (49) are given as
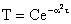
|
(50)
|
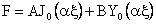
|
(51)
|
where 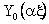 are
Bessel function of first and second kind of zeroth order. are
Bessel function of first and second kind of zeroth order.
The boundary conditions are
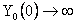 , ,
|
(52)
|
and
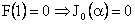 . .
|
(53)
|
Equation (53) is a characteristic equation. The corresponding eigenvalues, 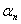 , are given as , are given as
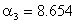 , ,
|
(54)
| The general solution for Equation (43) then is given by
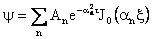 . .
|
(55)
|
Using the initial condition
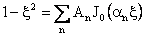
|
(55)
|
then
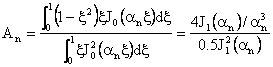
|
(56)
|
or
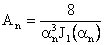
|
(57)
|
Hence,
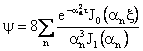
|
(58)
|
and
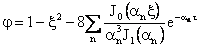
|
(59)
|
Variation of the velocity profile in the pipe is shown schematically in Figure 5.
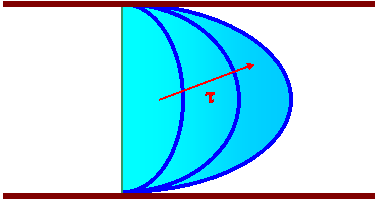
Figure 5. Variations of velocity field in a tube subject
to a step change in pressure. | 























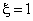
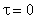
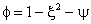
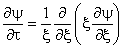
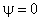 .
.
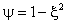 .
.
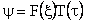
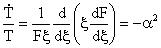 .
.
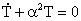 ,
,
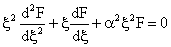 .
.
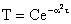
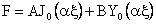
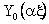 are
Bessel function of first and second kind of zeroth order.
are
Bessel function of first and second kind of zeroth order.
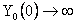 ,
,
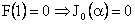 .
.
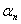 , are given as
, are given as
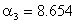 ,
,
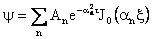 .
.