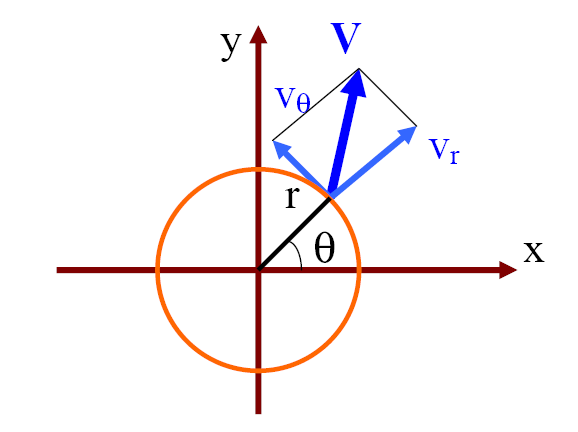
Incompressible Viscous Flows

Plane Flows in a Cylindrical Geometry

Case (a)

Figure 2. Schematics of plane flows in a polar coordinate system.

For a plane flow in cylindrical geometry as shown in Figure 2, let

That is,

or

The nonzero element of

where

Equation (7) now becomes

Using (17), Equation (19) may be restated as

or

;

Equation (21) is the equation governing

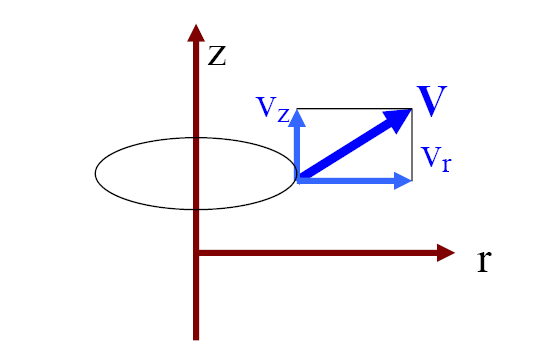
Figure 3. Schematics of axisymmetric flows in a cylindrical coordinate system.

For an axisymmetric flow in cylindrical coordinates, let

That is

or

The vorticity define by Equation (4) now becomes

Thus, the only nonzero component of vorticity is given by

where

Equation (7) may now be restated as

Using (26) in (28) we find

or

Equation (30) governs .
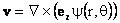
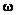
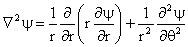
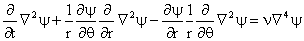
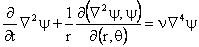
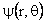
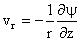
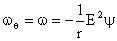
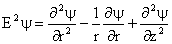
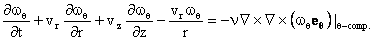
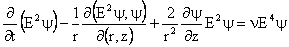
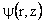