Hydrodynamic Forces and Torques for a Nonspherical Particle
Oblate Spheroid in a Uniform Flow
The solution satisfying both equations (27) and (28) is given as
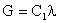
|
(29)
|
where
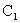 is a
constant. From (29) it follows that is a
constant. From (29) it follows that
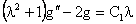
|
(30)
|
The general solution to equation (30), which is the summation of the
homogeneous and particular solutions, is given as
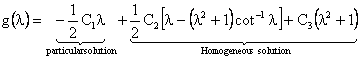
|
(31)
|
Using (31) in (22), the expression for the stream function becomes
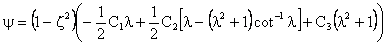
|
(32)
|
The constant 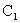 , ,
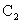 , and , and
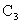 may now
be determined by using the boundary conditions given by (17) and (18). These become may now
be determined by using the boundary conditions given by (17) and (18). These become
The final expression for the stream function becomes
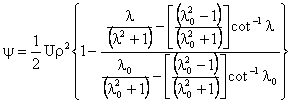
|
(34)
|
where 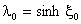 . . | 

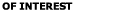






















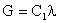
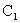 is a
constant. From (29) it follows that
is a
constant. From (29) it follows that
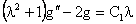
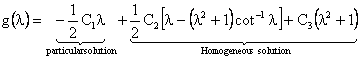
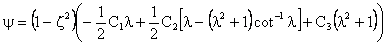
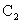 , and
, and
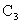 may now
be determined by using the boundary conditions given by (17) and (18). These become
may now
be determined by using the boundary conditions given by (17) and (18). These become
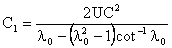 ,
,
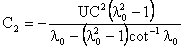 , and
, and
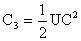
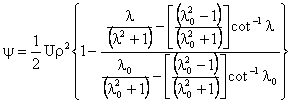
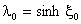 .
.