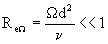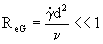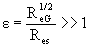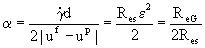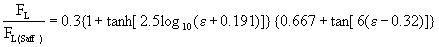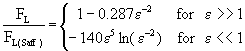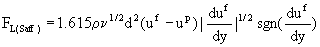

















|
|
|
Lift Force
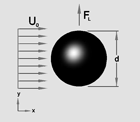
Small particles in a shear field as shown in Figure 1 experience a
lift force perpendicular to the direction of flow. The shear
lift originates from the inertia effects in the viscous flow around the
particle and is fundamentally different from the
aerodynamic lift force. The expression for the inertial shear lift was
first obtained my Saffman(1965.1968). That is
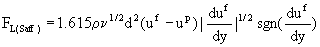 |
(1) |
|
|
| Calculation Model |
 |
Saffman Lift Force
|
 |
|
Here uƒ is the fluid velocity at the location of the
mass center of the particle, up is the particle
velocity, 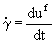 is the shear rate, d is the
particle diameter, and ρ and ν are the fluid density
and viscosity. Note that FL is in the positive-y direction
if uf>up. is the shear rate, d is the
particle diameter, and ρ and ν are the fluid density
and viscosity. Note that FL is in the positive-y direction
if uf>up.
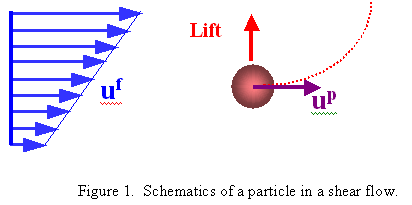 Equation 1 is subjected to the following constraints:
Here Ω is the rotational speed of the sphere. Dandy & Dwyer(1990) found that the Saffman lift force is approximately
valid at larger Res and small ε. McLaughlin(1991) showed that the lift force decreases as ε
decreases. Based on these studies, Mei(1992) suggested the following empirical fit to the results of Dandy and Dwyer and McLuaghlin.
For large ε and Res,
Equation 1 is subjected to the following constraints:
Here Ω is the rotational speed of the sphere. Dandy & Dwyer(1990) found that the Saffman lift force is approximately
valid at larger Res and small ε. McLaughlin(1991) showed that the lift force decreases as ε
decreases. Based on these studies, Mei(1992) suggested the following empirical fit to the results of Dandy and Dwyer and McLuaghlin.
For large ε and Res,

|
(2)
| where
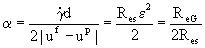
|
(3)
|
For 0.1<ε<20
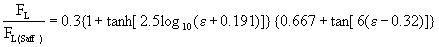
|
(4)
|
For large and small ε McLaughlin obtained the following expressions
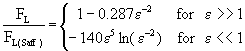
|
(5)
|
Note the change in sign of the lift force for the small values of ε.
|


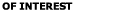


















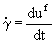 is the shear rate, d is the
particle diameter, and ρ and ν are the fluid density
and viscosity. Note that FL is in the positive-y direction
if uf>up.
is the shear rate, d is the
particle diameter, and ρ and ν are the fluid density
and viscosity. Note that FL is in the positive-y direction
if uf>up.