|
Particle Deposition Mechanisms: Impaction
Inertia Impactions
Near the stagnation point of an in-viscid flow the fluid velocity field is given by
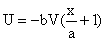
|
(1)
|
where b is a non-dimensional constant. For a particle under Stokes drag moving on the stagnation streamline, the equation of motion is given by
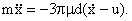
|
(2)
|
Using (1) in (2) and restating the resulting equation in a non-dimensional form, it follows that
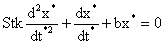
|
(3)
|
where the Stokes number is defined as
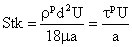
|
(4)
|
and
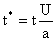
|
(5)
|
For the linear constant coefficient equation given by (3), the solution is given as
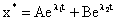
|
(6)
|
where 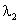 are the
solutions to the characteristic equation given by are the
solutions to the characteristic equation given by
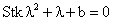
|
(7)
|
That is,
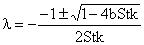
|
(8)
|
It is observed that for
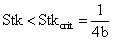
|
(9)
|
the roots are real and negative. This will lead to
vanishing of 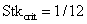 . Additional
details were provided by Friedlander (2000). . Additional
details were provided by Friedlander (2000).
| 

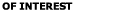






















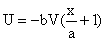
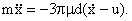
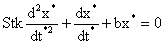
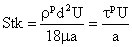
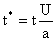
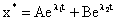
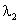 are the
solutions to the characteristic equation given by
are the
solutions to the characteristic equation given by
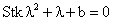
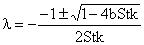
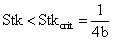
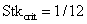 . Additional
details were provided by Friedlander (2000).
. Additional
details were provided by Friedlander (2000).